Exogenous inputs in Modelica are usually entered using the TimeTable or CombiTimeTable components. However, the inputs points being discrete in time, a time event is generated at each new data point.  This can considerably slow down the simulation and should therefore be avoided.

To address this issue, a possible solution consist in finding an analytical expression that can fit the data within an acceptable tolerance. For very simple data sets, it can be performed with a simple linear regression. However, for more complex inputs, even high-order polynomials cannot match the data in an acceptable way.

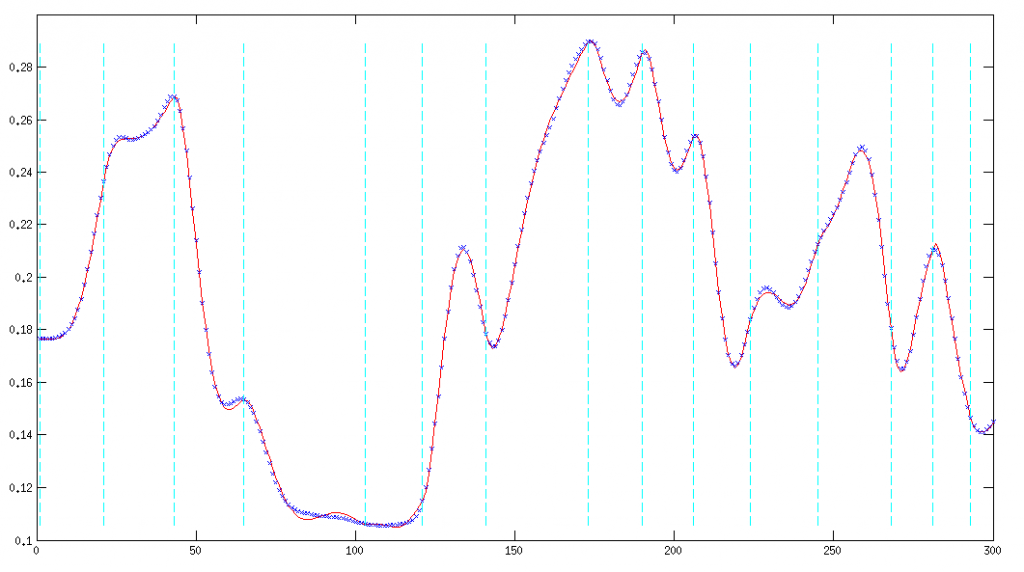
The SPPR tool uses a quadratic programming algorithm to optimize the boundaries of the intervals on which the regression is performed. The constraints of the optimization are twofold:

• Two adjacent polynomial regressions should have the same value on the boundary (the function must be continuous)
• Two adjacent polynomial regressions should have the same deriative on the boundary (the function must be C1-continuous)

This is illustrated in the figure below: the data points are indicated by blue crosses. The regression is indicated in red. The fitting intervals are delimited by the blue vertical lines. These intervals are optimized to achieve a user-defined accuracy between the polynomial regressions and the data.

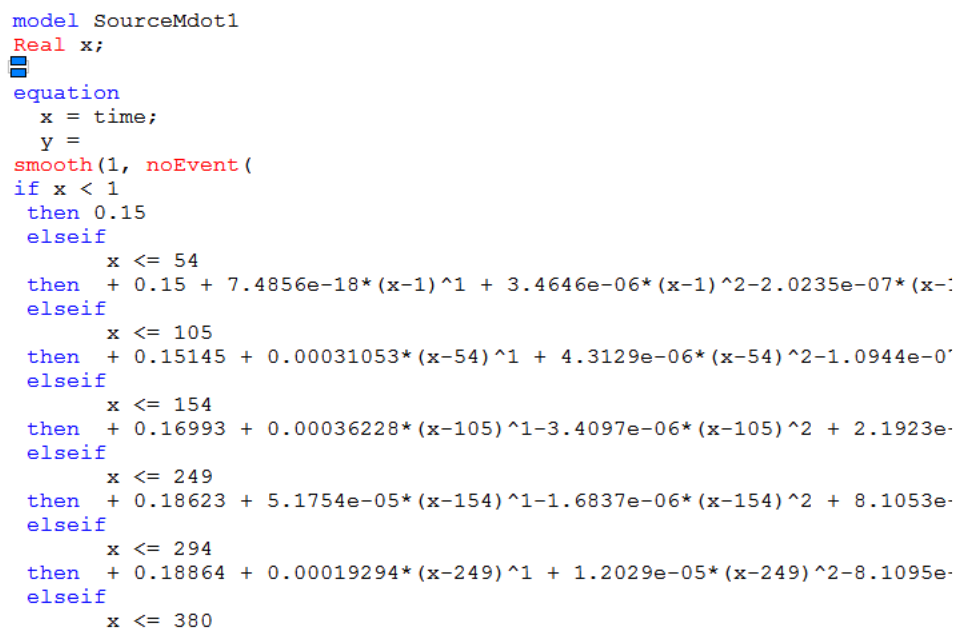
The tool then transforms the polynomial into Modelica code than can easily be copied and pasted into a Modelica component: